需求响应的新技术，你get了吗？-风光储氢-CPEM吉瓦风电网--风电行业门户网站

需求响应的新技术，你get了吗？

2019-07-19分类：风光储氢 / 风光储氢来源：阅读数：( )

引言

风电是目前发展前景最好的可再生能源发电方式之一[1], 但由于其出力随机性和不确定性的特点, 大规模风电并网将会给电网调度带来巨大挑战。随着未来智能电网中柔性负荷比例的不断提高, 通过需求响应(demand response, DR)来适应风电大规模接入系统, 将是未来智能电网的发展趋势[2-3]。

国内外学者针对需求侧资源参与风电消纳已开展了大量研究, 文献[3]在含风电电力系统的电网经济调度模型中考虑了价格型DR, 以降低常规机组的运行成本。文献[4-7]中提出了考虑DR参与电网调度以提升系统风电消纳水平的优化调度策略。文献[8-10]中以节能减排作为优化目标之一, 建立了考虑源荷互动的电力系统优化调度模型, 验证了价格型DR在提升环保效益方面的作用。然而, 上述文献均属于在传统优化调度模型中考虑确定性的DR参与调度。

在实际系统中, 价格型DR的调度效果受到诸多因素的影响[11-15], 其响应量存在不确定性。目前, 已有学者对价格型DR不确定性响应建模和考虑价格型DR不确定性的电力系统优化调度策略进行了研究。文献[11-12]以电价——负荷关系曲线为基础, 采用曲线上某点的随机误差来表示负荷变化量的随机性, 考虑了风电和价格型DR与机组组合的结合, 验证了价格型DR可以在一定程度上降低由风电出力不确定性给系统带来的不利影响。文献[13-14]通过期望值和随机误差之和的形式来表示价格型DR的调度量, 验证了价格型DR的不确定性会给系统可靠性带来不利影响。文献[15]基于消费者心理学模型, 建立了价格型DR模糊响应模型, 并提出了计及不确定性DR的日前调度计划模型。上述文献为价格型DR不确定性响应建模提供了良好的理论依据, 但文献中所建立的价格型DR不确定性模型不能充分反映影响价格型DR不确定性大小的因素, 且该影响因素对电力系统日前优化调度的影响分析也研究较少。

在进行风电出力和负荷响应不确定性的描述时, 已有文献较多从概率的角度出发[16-17]。然而, 采用概率的方式可能会出现以下问题:概率分布函数依赖于充足的信息, 在实际系统中, 可能存在风电出力、负荷响应信息不足或信息收集困难的情况, 因而难以精确建立概率分布函数。相对而言, 模糊数可以在信息不充分或没有任何现存的信息时借助专家系统得到不确定参数的隶属函数, 因此, 这也是一种较好的描述风电出力和负荷响应不确定性的方式[18]。

综上所述, 本文在已有研究的基础上[15, 19-23], 分析了影响价格型DR不确定性的重要因素, 在分时电价(time-of-use price, TOU)的环境下, 建立了基于模糊理论的价格型DR不确定性响应模型。在综合考虑价格型DR、风电出力和负荷预测值不确定性的基础上, 以常规机组运行成本和系统弃风成本最小为目标, 建立了电力系统模糊日前优化调度模型。通过对模型期望约束和模糊机会约束的等效处理, 将模糊优化模型转换成确定性模型, 通过仿真算例分析了考虑价格型DR不确定性、模糊机会约束置信度、负荷自弹性系数和电价激励水平引导程度对常规机组运行成本和系统弃风成本的影响。

1. TOU下的负荷模糊响应模型

1.1 响应不确定性的模糊表示

在TOU环境下, 常采用自弹性系数表征电价变化率对负荷变化率的影响, 自弹性系数定义为[3]:

$λ_{Δ q, t} = ε_{t t} λ_{Δ c, t}$

(1)

式中:λΔq, t为时段t的负荷响应率; λΔc, t为时段t的电价变化率; εtt为时段t的自弹性系数。

在实际需求响应过程中, 负荷的响应量通常无法完全确定, 其必然存在一定的不确定性[11-15], 实际负荷响应率可以采用模糊数进行表达。三角隶属度函数是研究不确定性问题时广泛采用的隶属度函数, 因此, 本文也采用三角隶属度函数来描述负荷响应率的不确定程度, 负荷响应率的三角隶属度函数表达示意图见附录A图A1。

负荷响应率的模糊表达式和隶属度参数之间的关系如下:

${\tilde{λ}}_{Δ q, t} = (λ_{Δ q 1, t}, λ_{Δ q 2, t}, λ_{Δ q 3, t})$

(2)

${\begin{cases} λ_{Δ q 2, t} = ε_{t t} λ_{Δ c, t} \\ λ_{Δ q 1, t} = λ_{Δ q 2, t} - d_{t} \\ λ_{Δ q 3, t} = λ_{Δ q 2, t} + d_{t} \end{cases}$

(3)

式中: $\tilde{λ}$ Δq, t为时段t负荷响应率的模糊表达形式; λΔq1, t, λΔq2, t, λΔq3, t为时段t负荷响应率的隶属度参数; dt为时段t预测负荷响应率的最大误差水平, dt≥0。

1.2 响应预测误差的变化机理

在实际情况中, TOU环境下的负荷响应误差范围将受到多方面因素的影响。

在TOU环境下, 负荷响应量预测问题可看作是在不同电价环境下的负荷预测问题, 因此, 负荷对电价响应量预测的不确定性在某种程度上与负荷预测的不确定性具有相似性, 故类比负荷预测模糊模型[19-21], 负荷响应率最大误差水平与负荷响应量成正相关[22]。

自弹性系数是能够体现负荷用电特性的参数, 其数值越大表示负荷的柔性程度越高。文献[22]中指出, 自弹性系数较大的负荷, 负荷的不确定响应范围较大; 自弹性系数较小的负荷, 负荷的不确定响应范围较小。因此, 在负荷模糊响应模型中, 本文采用正相关关系表征负荷响应率最大误差水平与负荷自弹性系数间的关系。

激励水平是影响负荷响应率预测误差的重要因素之一。文献[15]和文献[23]的研究结果表明, 当激励水平越高时, 用户受到利益的驱动作用越强, 价格因素逐渐成为影响用户用电方式的最主要引导因素, 负荷响应的不确定性随之降低; 反之, 外界环境因素对负荷响应率的影响程度将越来越大, 负荷响应不确定性增加。因此, 在负荷模糊响应模型中, 本文采用负相关关系表征负荷响应率最大误差水平与电价变化率间的关系。

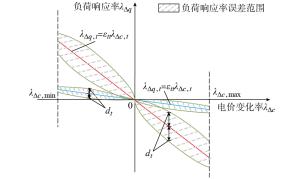
基于上述分析结果, 价格型DR负荷响应率误差范围如图 1所示。图中:红色和蓝色曲线表示自弹性系数不同的两种负荷的负荷响应率预测值, 假设红线代表负荷1、蓝线代表负荷2;阴影部分为负荷响应率误差范围, λΔc < 0表示削减电价, λΔc > 0表示增加电价; λΔc, min和λΔc, max分别表示电价变化率的下限和上限, 且λΔc, min < 0。随着电价变化率绝对值的增大, 负荷响应率预测值相应增大, 误差范围增加; 当电价变化率绝对值增大到一定程度时, 受电价的强引导作用, 误差范围有减少的趋势。总体而言, 误差范围有先增大后减小的趋势。由于负荷1的自弹性系数大于负荷2的自弹性系数, 因此, 负荷1的负荷响应误差范围更大。

图 1

图 1 价格型DR负荷响应率误差范围示意图

Figure 1. Schematic diagram of error range for price-based demand response load variation rate

下载: 全尺寸图片幻灯片

为了简化计算且能够综合表示上述规律, 本文采用两段直线来表征负荷响应量、自弹性系数和电价激励水平对负荷响应率最大误差系数的影响。负荷响应率最大误差水平的变化机理由式(4)表征。负荷响应率最大误差水平变化规律见附录A图A2。

$\begin{array}{l} d_{t} = \\ {\begin{matrix} \begin{array}{l} | k_{1} λ_{Δ q, t} | \\ | k_{1} λ_{Δ q}^{I P} + k_{2} λ_{Δ q, t} | \end{array} & \begin{array}{l} | λ_{Δ c, t} | \leq | λ_{Δ c}^{I P} | \\ | λ_{Δ c}^{I P} | \leq | λ_{Δ c, t} | \leq | λ_{Δ c, max / min} | \end{array} \end{matrix} \end{array}$

(4)

式中:λΔc, max/min表示电价变化率的上下限, 当λΔc大于0或小于0时, λΔc, max/min分别等于λΔc, max或λΔc, min; k1和k2分别为电价因素占据主导前和主导后最大误差水平与负荷响应变化率的比例系数; λΔcIP为拐点电价变化率, 当电价变化率绝对值大于拐点电价变化率绝对值后, 电价因素开始占据主导作用, 其绝对值与电价激励水平引导程度成负相关[15, 23]; λΔqIP为拐点电价变化率对应的负荷变化率预测值。

k1和k2均与负荷自弹性系数成正相关[22]。由于k1表示电价因素占据主导前的比例系数, 因此, 本模型中假设电价激励水平引导程度对k1的影响可以忽略不计; 而k2表示电价因素占据主导后的比例系数, 因此, k2与电价激励水平引导程度成负相关[15, 23]。k1, k2和λΔqIP直接影响负荷响应率的隶属度参数, 其值可以根据历史数据获得, 当历史数据不充分或没有任何现存的信息时, 也可以借助专家系统获得[18, 21, 24-25]。

将式(4)代入式(3)即可得到负荷模糊响应模型, 该模型可以表征不同自弹性系数和受电价激励水平引导程度不同的负荷的响应不确定性情况。

2. 考虑风电消纳效益的源荷互动模糊日前优化调度模型

2.1 风电出力及负荷预测值的三角模糊表示

各调度周期内的风电出力与系统负荷也可以采用三角模糊数表示。风电出力和系统负荷的模糊表达式和隶属度参数之间的关系如下[24-25]:

$\tilde{P} = (P_{1}, P_{2}, P_{3})$

(5)

${\begin{cases} P_{2} = P_{f, t} \\ P_{1} = r_{1} P_{f, t} \\ P_{3} = r_{3} P_{f, t} \end{cases}$

(6)

式中: $\tilde{P}$ 为风电出力和系统负荷的模糊表达式; P1, P2, P3为风电出力和系统负荷的三角隶属度参数; Pf, t为t时段风电和负荷的预测值; r1和r3为比例系数, 且0 < r1 < 1, r3 > 1, 比例系数一般可以由风电和负荷的历史数据确定[24-25]。

考虑负荷预测值为模糊数时, 负荷响应量的预测值也应该为模糊数, 计算公式如下。

$Δ {\tilde{q}}_{f, t} = ε_{t t} λ_{Δ c, t} {\tilde{P}}_{L, t} Δ t$

(7)

式中:Δ $\tilde{q}$ f, t为时段t负荷响应量预测值的模糊表达式; $\tilde{P}$ L, t为时段t负荷预测值的模糊表达式; Δt为一个调度时段的时长。

由于通常情况下负荷的预测值误差较小, 即负荷的比例系数r1和r3均较接近1, 因此, 为了简化运算, 将负荷响应量的预测值用负荷预测值的确定形式表示, 表达式如下。

$Δ q_{f, t} = ε_{t t} λ_{Δ c, t} P_{f L, t} Δ t$

(8)

式中:Δqf, t为时段t的负荷响应量预测值; PfL, t为时段t的负荷预测值。

2.2 目标函数

目标函数考虑最小化系统运行成本。

$min F = F_{1} + F_{inf, 2}$

(9)

式中:F为系统运行成本; F1为常规机组运行成本; Finf, 2为系统弃风成本的悲观值, 其含义是指, 在一定置信度条件下, 大于弃风成本模糊变量的最小弃风成本[26]。

1) 常规机组运行成本

${\begin{cases} F_{1} = \sum_{t = 1}^{T} \sum_{i = 1}^{N_{G}} [f_{i} (P_{G i, t}) u_{i, t} + S_{i, t} (1 - u_{i, t - 1}) u_{i, t}] \\ f_{i} (P_{G i, t}) = a_{i} P_{G i, t}^{2} + b_{i} P_{G i, t} + c_{i} \end{cases}$

(10)

式中: NG为常规机组总台数; fi为常规机组i的运行成本; PGi, t为常规机组i在时段t的输出功率; Si, t为常规机组i在时段t的开机成本; ui, t和ui, t-1分别为常规机组i的当前时刻与前一时刻的启停状态, 若机组为开机状态则ui, t=1, 反之ui, t=0;ai, bi, ci为常规机组i的运行费用参数。

2) 弃风成本

${\begin{cases} {\tilde{F}}_{2} = \sum_{t = 1}^{T} c_{w} ({\tilde{P}}_{W, t} - {\tilde{P}}_{W s, t}) Δ t \\ F_{inf, 2} = inf {r | C r {{\tilde{F}}_{2} \leq r} \geq α} \end{cases}$

(11)

式中: $\tilde{F}$ 2为系统弃风成本的模糊表达式; cw为系统单位弃风成本; $\tilde{P}$ W, t为时段t的风电调度出力模糊表达式; $\tilde{P}$ Ws, t为时段t调度指令下发后的风电出力(以下简称调度后风电出力)模糊表达式; inf{}为取下界符号; Cr{}为置信度表达式; r为变量; α为悲观值置信度[26]。

其中, 调度后风电出力为三角模糊数, 模糊参数取值规则如下:

${\begin{cases} P_{W s 1, t} = P_{W s, t}, P_{W s 2, t} = P_{W s, t}, P_{W s 3, t} = P_{W s, t} \\ 0 \leq P_{W s, t} \leq P_{W 1, t} \\ P_{W s 1, t} = P_{W 1, t}, P_{W s 2, t} = P_{W s, t}, P_{W s 3, t} = P_{W s, t} \\ P_{W 1, t} < P_{W s, t} \leq P_{W 2, t} \\ P_{W s 1, t} = P_{W 1, t}, P_{W s 2, t} = P_{W 2, t}, P_{W s 3, t} = P_{W s, t} \\ P_{W 2, t} < P_{W s, t} \leq P_{W 3, t} \end{cases}$

(12)

式中:PWs1, t, PWs2, t, PWs3, t为调度后风电出力的隶属度参数; PW1, t, PW2, t, PW3, t为风电预测出力的隶属度参数, PW2, t等于时段t风电出力预测值, 即PfW, t; PWs, t为时段t的风电调度出力指令值。

该取值规则的意义为:实际运行中, 当风电出力大于风电调度出力指令值PWs, t时, 会弃掉多余部分风电, 即大于风电调度出力指令值的隶属度为0;当风电出力小于风电调度出力指令值时, 隶属度参数保持不变。

2.3 约束条件

1) 系统约束

从上到下分别为系统负荷平衡约束、系统正旋转备用约束和系统负旋转备用约束:

${\begin{cases} \sum_{i = 1}^{N_{G}} P_{G i, t} + E ({\tilde{P}}_{W s, t}) = E ({\tilde{P}}_{L, t}) + E (\frac{Δ {\tilde{q}}_{t}}{Δ t}) \\ C r {\sum_{i = 1}^{N_{G}} u_{i, t} min (P_{G i, max}, P_{G i, t} + R_{i, u p}) + \\ {\tilde{P}}_{W s, t} \geq {\tilde{P}}_{L, t} + \frac{Δ {\tilde{q}}_{t}}{Δ t}} \geq β \\ C r {\sum_{i = 1}^{N_{G}} u_{i, t} max (P_{G i, min}, P_{G i, t} - R_{i, d o w n}) + \\ {\tilde{P}}_{W s, t} \leq {\tilde{P}}_{L, t} + \frac{Δ {\tilde{q}}_{t}}{Δ t}} \geq γ \end{cases}$

(13)

式中: E(ξ)为模糊数ξ的期望; $\tilde{P}$ L, t为时段t的系统负荷模糊表达式; PGi, max和PGi, min分别为常规机组i的出力上限和下限; Ri, up和Ri, down分别为常规机组i的单位时间向上爬坡和向下爬坡功率; β和γ分别为满足正旋转备用约束和负旋转备用约束的置信度; Δ $\tilde{q}$ t为时段t的负荷响应量模糊表达式。

Δ $\tilde{q}$ t与 $\tilde{λ}$ Δq, t的关系如式(14)所示, 可知Δ $\tilde{q}$ t依然为三角模糊数。

$Δ {\tilde{q}}_{t} = {\tilde{λ}}_{Δ q, t} P_{f L, t} Δ t$

(14)

当系统风电渗透率较高时, 常规机组为了防止风电出力突然下降而出现“失负荷”现象, 需要开启一定数量的机组满足系统正旋转备用约束, 但当风电出力突然上升后, 受常规机组爬坡能力和最小出力的限制, 系统可能无法接受突然增大的风电出力, 则可能会出现弃风现象。因此, 在式(13)正、负旋转备用约束中, 风电出力表达式选择风电调度出力模糊表达式而非风电出力模糊表达式, 风电出力模糊表达式与风电调度出力模糊表达式之差即为该时段弃风量的模糊表达式。

2) 常规机组约束[27]

${\begin{cases} P_{G i, min} \leq P_{G i, t} \leq P_{G i, max} \\ P_{G i, t} - P_{G i, t - 1} \leq R_{i, u p} \\ P_{G i, t - 1} - P_{G i, t} \leq R_{i, d o w n} \\ T_{i, t}^{o n} \geq T_{i, min}^{o n} \\ T_{i, t}^{o f f} \geq T_{i, min}^{o f f} \end{cases}$

(15)

式中:Ti, ton和Ti, toff分别为常规机组i在时段t前的持续运行时间和持续停机时间; Ti, minon和Ti, minoff分别为常规机组i的最小持续运行时间和最小持续停机时间。

3) 价格型DR约束[13]

式(16)从上到下分别表示电价约束和电量平衡约束:

${\begin{cases} λ_{Δ c, min} \leq λ_{Δ c, t} \leq λ_{Δ c, max} \\ E (\sum_{t = 1}^{T} Δ {\tilde{q}}_{t}) = 0 \end{cases}$

(16)

3. 模型求解

3.1 模糊期望约束的确定性表达式

本文提出的优化调度模型中, 等式约束(系统负荷平衡约束、调度电量平衡约束)采用模糊期望约束的形式表示。系统负荷平衡约束和调度电量平衡约束经三角模糊数的期望计算公式[26]化简后可以转换为确定性约束, 转换后的系统负荷平衡约束和调度电量平衡约束分别如式(17)和式(18)所示。

$\begin{array}{l} \sum_{i = 1}^{N_{G}} P_{G i, t} + \frac{1}{4} (P_{W s 1, t} + 2 P_{W s 2, t} + P_{W s 3, t}) = \\ \frac{1}{4} (P_{L 1, t} + P_{L 2, t} + P_{L 3, t}) + \\ \frac{1}{4} (\frac{Δ q_{1 t}}{Δ t} + 2 \frac{Δ q_{2 t}}{Δ t} + \frac{Δ q_{3 t}}{Δ t}) \end{array}$

(17)

$\sum_{t = 1}^{T} \frac{1}{4} (Δ q_{1 t} + 2 Δ q_{2 t} + Δ q_{3 t}) = 0$

(18)

式中: PL1, t, PL2, t, PL3, t为系统负荷的隶属度参数; Δqt1, Δqt2, Δqt3为价格型DR负荷响应量的隶属度参数。

3.2 模糊机会约束的清晰等价类转换

本文提出的优化调度模型中, 弃风成本悲观值约束和系统正(负)旋转备用约束采用模糊机会约束的形式表达, 其可以通过转换成为清晰等价类的方式转换为确定性约束。能够转换成清晰等价类的标准模糊机会约束形式为[26]:

${\begin{cases} C r {g (x, ξ) \leq 0} \geq α \\ g (x, ξ) = h_{1} (x) ξ_{1} + h_{2} (x) ξ_{2} + \dots + \\ h_{n} (x) ξ_{n} + h_{0} (x) \end{cases}$

(19)

式中:g(x, ξ)为约束条件; x为确定性变量; ξ为梯形模糊变量或三角模糊变量; hn(x)为x的函数。

由式(11)和式(13)可知, 上述模糊机会约束均满足标准形式, 可以直接转换成清晰等价类形式。转换的详细步骤参见文献[26]。

转换后的弃风弃光成本悲观值表达式如式(20)所示。

$\begin{array}{l} F_{inf, 2} = (2 - 2 α) \sum_{t = 1}^{T} c_{w} (P_{W 2, t} - P_{W s 2, t}) + \\ (2 α - 1) \sum_{t = 1}^{T} c_{w} (P_{W 3, t} - P_{W s 1, t}) \end{array}$

(20)

转换后的系统正(负)旋转备用约束如式(21)所示。

${\begin{cases} (2 - 2 β) (P_{L 2, t} + \frac{Δ q_{2 t}}{Δ t} - P_{W s 2, t}) + \\ (2 β - 1) (P_{L 3, t} + \frac{Δ q_{3 t}}{Δ t} - P_{W s 1, t}) \leq \\ \sum_{i = 1}^{N_{G}} u_{i, t} min (P_{G i, max}, P_{G i, t} + R_{i, u p}) \\ (2 - 2 γ) (P_{L 2, t} + \frac{Δ q_{2 t}}{Δ t} - P_{W s 2, t}) + \\ (2 γ - 1) (P_{L 1, t} + \frac{Δ q_{1 t}}{Δ t} - P_{W s 3, t}) \geq \\ \sum_{i = 1}^{N_{G}} u_{i, t} max (P_{G i, min}, P_{G i, t} - R_{i, d o w n}) \end{cases}$

(21)

经过对模糊约束条件的处理, 本文提出的模糊优化模型可以转换为确定性优化模型, 转换后的优化调度问题为混合整数规划问题, 采用商业优化软件即可进行求解。本文采用商业优化软件ILOG CPLEX 12.6.3进行求解。

4. 算例分析

4.1 算例数据

本文采用一个含风电场及10台常规机组的电力系统数据为算例进行仿真分析。一个调度周期选取24个调度时段; 10台常规机组的参数见文献[27]; 风电场预测出力和负荷预测大小见附录A表A1;风电出力及负荷预测值的三角隶属度参数取值见附录A表A2[24]。

假设系统负荷自弹性系数为-0.2[3]; 电价变化率的下限和上限分别为-0.5和0.5;最大误差水平与负荷响应变化率的比例系数为k1=0.5, k2=0;拐点电价变化率为±0.3;单位弃风电价为500元/(MW·h)。

弃风成本悲观值置信度α取0.9;正(负)旋转备用约束置信度β和γ均取0.95。

4.2 考虑负荷调度不确定性的影响分析

为了对比分析负荷模糊响应模型参与电力系统优化调度后的效果, 设置了3个优化场景:场景1中不考虑价格型DR参与系统调度; 场景2中考虑价格型DR参与系统调度, 但不考虑价格型DR的不确定性; 场景3中考虑了价格型DR的不确定性。

不同场景下常规机组启停成本、常规机组燃料成本、弃风成本和系统总运行成本如表 1所示。不同场景下各时段弃风量悲观值(置信度为0.9)如附录A图A3所示。不同场景下各时段负荷响应量预测值如附录A图A4所示。

表 1

表 1 不同场景下的成本对比

Table 1. Comparison of costs under different scenarios

下载: 导出CSV

经过对表 1、附录A图A3和图A4的分析可以得出如下结论。

1) 在场景1中, 完全依靠常规机组消纳风电会迫使常规机组频繁启停, 并开启运行经济性较差的机组, 运行成本较高, 且并不能取得很好的消纳效果。

2) 在场景2和3中, 当价格型DR参与系统优化调度后, 可以在风电出力较高的时段降低电价, 增加负荷, 消纳多余的风电出力, 减小系统弃风成本。此外, 还可以在适当的时段通过增加电价、削减负荷、减小经济性较差的机组出力, 提升常规机组运行经济性。

3) 在场景3中, 考虑价格型DR不确定性后, 价格型DR消纳风电的能力有所下降, 但其依然能够与常规机组配合, 降低常规机组的运行成本。

4.3 模糊机会约束置信度的影响分析

在场景3下, 选取不同正(负)旋转备用约束置信度, 计算系统运行成本, 计算结果如表 2所示。

表 2

表 2 不同置信度下的成本对比

Table 2. Comparison of costs under different confidence levels

下载: 导出CSV

经过对表 2的分析可以得出如下结论。

1) 约束条件置信水平反映了对约束条件越限的风险把握。随着旋转备用约束置信水平的下降, 启停成本、燃料成本和弃风成本均有所下降, 但降低置信水平可能导致系统承担更大的运行风险。

2) 该系统发生弃风现象的主要原因是:由于风电出力的不确定性, 常规机组无法兼顾正旋转备用和负旋转备用。因此, 弃风成本受系统旋转备用约束严苛程度的影响较大, 当约束置信水平下降时, 弃风成本的变化程度最为明显。

4.4 自弹性系数和电价激励水平引导程度的影响分析

1) 自弹性系数对系统运行成本的影响分析

在场景3的基础上, 假设系统负荷自弹性系数分别为-0.1, -0.2, -0.3和-0.4;由于比例系数与自弹性系数成正相关[22], 因此假设对应的比例系数分别为: k1=0.25, k2=-0.1;k1=0.5, k2=0;k1=0.75, k2=0.1和k1=1, k2=0.2, 其余条件不变。考虑不确定性前后的系统运行成本如表 3所示。

表 3

表 3 考虑不确定性前后不同弹性系数下的成本对比

Table 3. Comparison of costs with different elasticity factors before and after considering uncertainty

下载: 导出CSV

对表 3进行分析可得出如下结论:①当不考虑价格型DR不确定性时, 提高负荷的弹性相当于提高了可调度负荷的容量, 其可以有效降低系统运行成本, 尤其是弃风成本; ②当考虑了价格型DR不确定性后, 提高负荷的弹性不但相当于提高了可调度容量, 而且增加了价格型DR的不确定性, 当负荷弹性过大时, 常规机组会承受更大的由旋转备用约束带来的压力, 因此反而会降低负荷参与系统优化调度的效果, 尤其是对弃风成本的优化效果。

2) 不同电价激励水平引导程度对系统运行成本的影响分析

在场景3的基础上, 假设电价激励水平引导程度的等级分别为强、中、弱, 由于拐点电价变化率绝对值和比例系数k2与负荷受电价激励水平引导程度成负相关[15, 23], 因此假设对应的拐点电价变化率分别±0.1, ±0.3和±0.5, 自弹性系数依然取-0.2, 比例系数k1依然为0.5, 比例系数k2分别为-0.1, 0, 0.1, 其余条件不变。不同拐点电价下的系统运行成本如表 4所示。

表 4

表 4 不同电价激励水平引导程度下的成本对比

Table 4. Comparison of costs with different electricity price guidance degrees

下载: 导出CSV

电价激励水平的引导作用越强, 价格型DR不确定性在一定程度上越会被削弱。由表 4可以看出, 随着电价激励水平引导作用的减弱, 即随着拐点电价变化率绝对值和比例系数k2的增大, 价格型DR对弃风成本的优化效果越会受到限制。

5. 结论

本文考虑了负荷响应量、负荷自弹性系数和电价激励水平对价格型DR不确定性的影响, 建立了价格型DR的模糊响应模型, 并在此基础上建立了考虑风电消纳效益的电力系统模糊日前优化调度模型, 基于仿真算例结果分析了价格型DR不确定性对电力系统日前优化调度的影响。得出如下结论。

1) 价格型DR的响应不确定性会削弱其消纳风电的能力, 但其依然能够与常规机组配合, 降低常规机组的运行成本。

2) 旋转备用约束置信度是影响系统运行成本的关键因素, 尤其是系统弃风成本; 降低置信度能够降低系统运行成本, 但同时也会使系统承受更大的安全风险。

3) 在一定程度上, 增大负荷的自弹性系数有利于风电的消纳; 但当自弹性系数过大时, 受价格型DR不确定性的影响, 价格型DR消纳风电的能力可能反而会有所削弱。

4) 负荷受电价激励水平的引导作用越强, 价格型DR响应不确定性越小, 消纳风电能力越强。

影响价格型DR不确定性的因素众多, 本文中仅就负荷响应量、负荷自弹性系数和电价激励水平的影响进行了研究。而价格型DR不确定性对电力系统优化调度效果有着重要影响, 价格型DR的响应不确定性模型需要进一步研究。

本文得到国网湖北省电力公司科技项目(52153815000D)资助, 谨此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1]
孙元章, 吴俊, 李国杰.风力发电对电力系统的影响[J].电网技术, 2007, 31(20):55-62.
SUN Yuanzhang, WU Jun, LI Guojie. Influence research of wind power generation on power systems[J]. Power System Technology, 2007, 31(20): 55-62.
[2]
姚建国, 杨胜春, 王珂, 等.智能电网"源-网-荷"互动运行控制概念及研究框架[J].电力系统自动化, 2012, 36(21):1-6.
YAO Jianguo, YANG Shengchun, WANG Ke, et al. Concept and research framework of smart grid "source-grid-load" interactive operation and control[J]. Automation of Electric Power Systems, 2012, 36(21): 1-6.
[3]
别朝红, 胡国伟, 谢海鹏, 等.考虑需求响应的含风电电力系统的优化调度[J].电力系统自动化, 2014, 38(13):115-120.DOI:10.7500/AEPS20131014001.
BIE Zhaohong, HU Guowei, XIE Haipeng, et al. Optimal scheduling of having wind farm power system considering demand respond[J]. Automation of Electric Power Systems, 2014, 38(13): 115-120. DOI: 10.7500/AEPS20131014001.
[4]
曾丹, 姚建国, 杨胜春, 等.应对风电消纳中基于安全约束的价格型需求响应优化调度建模[J].中国电机工程学报, 2014, 34(31):1-8.
ZENG Dan, YAO Jianguo, YANG Shengchun, et al. Optimization dispatch modeling for price-based demand response considering security constraints to accommodate the wind power[J]. Proceedings of the CSEE, 2014, 34(31): 1-8.
[5]
刘文颖, 文晶, 谢昶, 等.考虑风电消纳的电力系统源荷协调多目标优化方法[J].中国电机工程学报, 2015, 35(5):1079-1088.
LIU Wenying, WEN Jing, XIE Chang, et al. Multi-objective optimal method considering wind power accommodation based on source-load coordination[J]. Proceedings of the CSEE, 2015, 35(5): 1079-1088.
[6]
文晶, 刘文颖, 谢昶, 等.计及风电消纳效益的电力系统源荷协调二层优化模型[J].电工技术学报, 2015, 30(8):247-256. doi: 10.3969/j.issn.1000-6753.2015.08.031
WEN Jing, LIU Wenying, XIE Chang, et al. Source-load coordination optimal model considering wind power consumptive benefits based on bi-level programming[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 247-256. doi: 10.3969/j.issn.1000-6753.2015.08.031
[7]
杨楠, 王波, 刘涤尘, 等.考虑柔性负荷调峰的大规模风电随机优化调度方法[J].电工技术学报, 2013, 28(11):231-238. doi: 10.3969/j.issn.1000-6753.2013.11.032
YANG Nan, WANG Bo, LIU Dichen, et al. Large-scale wind power stochastic optimization scheduling method considering flexible load peaking[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 231-238. doi: 10.3969/j.issn.1000-6753.2013.11.032
[8]
曾鸣, 杨雍琦, 向红伟, 等.兼容需求侧资源的"源-网-荷-储"协调优化调度模型[J].电力自动化设备, 2016, 36(2):102-111.
ZENG Ming, YANG Yongqi, XIANG Hongwei, et al. Optimal dispatch model based on coordination between 'generation-gird-load-energy storage' and demand-side resource[J]. Electric Power Automation Equipment, 2016, 36(2): 102-111.
[9]
MADAENI S H, SIOSHANSI R. Using demand response to improve the emission benefits of wind[J]. IEEE Trans on Power Systems, 2013, 28(2): 1385-1394. doi: 10.1109/TPWRS.2012.2214066
[10]
刘晓, 艾欣, 彭谦.计及需求响应的含风电场电力系统发电与碳排放权联合优化调度[J].电网技术, 2012, 36(1):213-218.
LIU Xiao, AI Xin, PENG Qian. Optimal dispatch coordinating power generation with carbon emission permit for wind farms integrated power grid considering demand response[J]. Power System Technology, 2012, 36(1): 213-218.
[11]
WANG Q, WANG J, GUAN Y. Stochastic unit commitment with uncertain demand response[J]. IEEE Trans on Power Systems, 2013, 28(1): 562-563. doi: 10.1109/TPWRS.2012.2202201
[12]
ZHAO C, WANG J, WATSON J P, et al. Multi-stage robust unit commitment considering wind and demand response uncertainties[J]. IEEE Trans on Power Systems, 2012, 28(3): 2708-2717.
[13]
牛文娟, 李扬, 王蓓蓓.考虑不确定性的需求响应虚拟电厂建模[J].中国电机工程学报, 2014, 34(22):3630-3637.
NIU Wenjuan, LI Yang, WANG Beibei. Demand response based virtual power plant modeling considering uncertainty[J]. Proceedings of the CSEE, 2014, 34(22): 3620-3637.
[14]
刘小聪, 王蓓蓓, 李扬, 等.计及需求侧资源的大规模风电消纳随机机组组合模型[J].中国电机工程学报, 2015, 35(14):3714-3723.
LIU Xiaocong, WANG Beibei, LI Yang, et al. Stochastic unit commitment model for high wind power integration considering demand side resources[J]. Proceedings of the CSEE, 2015, 35(14): 3714-3723.
[15]
孙宇军, 李扬, 王蓓蓓, 等.计及不确定性需求响应的日前调度计划模型[J].电网技术, 2014, 38(10):2708-2714.
SUN Yujun, LI Yang, WANG Beibei, et al. A day-ahead scheduling model considering demand response and its uncertainty[J]. Power System Technology, 2014, 38(10): 2708-2714.
[16]
张宁宇, 高山, 赵欣.一种考虑风电随机性的机组组合模型及其算法[J].电工技术学报, 2013, 28(5):22-29. doi: 10.3969/j.issn.1000-6753.2013.05.003
ZHANG Ningyu, GAO Shan, ZHAO Xin. A unit commitment model and algorithm with randomness of wind power[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 22-29. doi: 10.3969/j.issn.1000-6753.2013.05.003
[17]
HETZER J, YU D C, BHATTARAI K. An economic dispatch model incorporating wind power[J]. IEEE Trans on Energy Conversion, 2008, 23(2): 603-611. doi: 10.1109/TEC.2007.914171
[18]
段翩, 朱建全, 刘明波.基于双层模糊机会约束规划的虚拟电厂优化调度[J].电工技术学报, 2016, 31(9):58-67. doi: 10.3969/j.issn.1000-6753.2016.09.008
DUAN Pian, ZHU Jianquan, LIU Mingbo. Optimal dispatch of virtual power plant based on bi-level fuzzy chance constrained programming[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 58-67. doi: 10.3969/j.issn.1000-6753.2016.09.008
[19]
BUNN D W. Forecasting loads and prices in competitive power markets[J]. Proceedings of the IEEE, 2000, 88(2): 163-169. doi: 10.1109/5.823996
[20]
ATTAVIRIYANUPAP P, KITA H, TANAKA E, et al. A fuzzy-optimization approach to dynamic economic dispatch considering uncertainties[J]. IEEE Trans on Power Systems, 2004, 19(3): 1299-1307. doi: 10.1109/TPWRS.2004.831272
[21]
陈海焱, 陈金富, 段献忠.含风电场电力系统经济调度的模糊建模及优化算法[J].电力系统自动化, 2006, 30(2):22-26. doi: 10.3321/j.issn:1000-1026.2006.02.004
CHEN Haiyan, CHEN Jinfu, DUAN Xianzhong. Fuzzy modeling and optimization algorithm on dynamic economic dispatch in wind power integrated system[J]. Automation of Electric Power Systems, 2006, 30(2): 22-26. doi: 10.3321/j.issn:1000-1026.2006.02.004
[22]
曾丹, 姚建国, 杨胜春, 等.计及价格型负荷响应不确定性的概率潮流计算[J].电力系统自动化, 2015, 39(20):66-71.DOI:10.7500/AEPS20141125005.
ZENG Dan, YAO Jianguo, YANG Shengchun, et al. Probabilistic load flow calculation considering price-elasticity load uncertainties[J]. Automation of Electric Power Systems, 2015, 39(20): 66-71. DOI: 10.7500/AEPS20141125005.
[23]
王蓓蓓, 孙宇军, 李扬.不确定性需求响应建模在电力积分激励决策中的应用[J].电力系统自动化, 2015, 39(10):93-99.DOI:10.7500/AEPS20140705006.
WANG Beibei, SUN Yujun, LI Yang. Application of uncertain demand response modeling in power-score incentive decision[J]. Automation of Electric Power Systems, 2015, 39(10): 93-99. DOI: 10.7500/AEPS20140705006.
[24]
艾欣, 刘晓, 孙翠英.含风电场电力系统机组组合的模糊机会约束决策模型[J].电网技术, 2011, 35(12):202-207.
AI Xin, LIU Xiao, SUN Cuiying. A fuzzy chance constrained decision model for unit commitment of power grid containing large-scale wind farm[J]. Power System Technology, 2011, 35(12): 202-207.
[25]
熊虎, 向铁元, 陈红坤, 等.含大规模间歇式电源的模糊机会约束机组组合研究[J].中国电机工程学报, 2013, 33(13):36-44.
XIONG Hu, XIANG Tieyuan, CHEN Hongkun, et al. Research of fuzzy chance constrained unit commitment containing large-scale intermittent power[J]. Proceedings of the CSEE, 2013, 33(13): 36-44.
[26]
刘宝碇.不确定规划及应用[M].北京:清华大学出版社, 2003.
[27]
TING T O, RAO M V C, LOO C K. A novel approach for unit commitment problem via an effective hybrid particle swarm optimization[J]. IEEE Trans on Power Systems, 2006, 21(1): 411-418. doi: 10.1109/TPWRS.2005.860907

来源：AEPS

分享到：

上一篇：河池市2022年风力和光伏发电项目：风电建设4890MW，光伏建设6315MW

下一篇：智能制造总论

编辑推荐